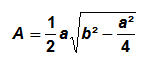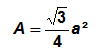Unités d’aire et de superficie
La surface désigne la couche superficielle d’un objet.
L’aire ou la superficie d’une surface correspond au nombre de points qui composent cette surface. Le terme aire est utilisé en mathématique alors que le terme superficie est utilisé principalement pour la mesure de la surface de terrains.
Unité de base : le mètre carré
Le mètre carré (symbole m²) est l’unité de base pour la mesure d’une aire. 1 mètre carré correspond à la surface d’un carré d’un mètre de côté.