Aire et surface d’un triangle rectangle
Dans un triangle rectangle, soient L et l les longueurs des côtés adjacents à l’angle droit. L’aire A de ce triangle rectangle est calculée à partir de la formule suivante :
A = L x l / 2
Aire et surface d’un triangle quelconque
Soit un triangle quelconque dont la hauteur est égale à h et la longueur de la base est L. L’aire A de ce triangle est égale à :
A = L x h / 2
Théorème de Pythagore
Théorème de Pythagore : dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit.
c² = a² + b²
Aire et surface d’un triangle isocèle
Un triangle isocèle est un triangle ayant au moins deux côtés de même longueur. Si b est la longueur de ces deux côtés et a la longueur du troisième côté, alors l’aire A correspondant à la surface de ce triangle isocèle est égale à :
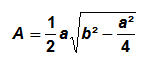
Un triangle isocèle ayant les propriétés d’un triangle quelconque, si h est la hauteur du triangle isocèle, son aire A est égale à :
A = a x h / 2
Aire et surface d’un triangle équilatéral
Un triangle équilatéral est un triangle dont les trois côtés sont égaux. Si a est la longueur de ces trois côtés, l’aire A correspondant à la surface de ce triangle équilatéral est égale à :
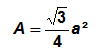
Un triangle équilatéral ayant les propriétés d’un triangle quelconque, si h est la hauteur du triangle équilatéral, son aire A est égale à :
A = a x h / 2
Périmètre du triangle
Soit un triangle dont les longueurs des trois côtés sont l1, l2 et l3. Le périmètre P de ce triangle est égal à la somme de la longueur de ses côtés, soit :
P = l1 + l2 + l3
Calcul de l’aire d’un triangle sans connaître sa hauteur
Comment calculer l’aire d’un triangle sans connaître sa hauteur ?
Longueur de la génératrice d’un cône
La génératrice d’un cône de révolution est un segment reliant le sommet du cône à un point du cercle formant la base de ce cône.
Le calcul de la longueur c de la génératrice d’un cône de révolution de rayon r et de hauteur H est effectué à partir de la formule suivante :
