Le nombre Pi
Le nombre Pi est représenté par lettre du même nom de l’alphabet grec : π.
π est un nombre constant dont la valeur est le rapport entre la circonférence d’un cercle et son diamètre. Sa valeur arrondie à 8 chiffres après la virgule est 3,14159265.
Surface et cercle : aire d’un disque
La surface délimitée par un cercle de rayon r correspond à l’aire A du disque de rayon r.
L’aire A d’un disque de rayon r est égale à :
A = π r ²
Aire et surface d’un triangle quelconque
Soit un triangle quelconque dont la hauteur est égale à h et la longueur de la base est L. L’aire A de ce triangle est égale à :
A = L x h / 2
Volume d’un cylindre
Le calcul du volume V d’un cylindre de diamètre d et de hauteur h est effectué à partir de la formule suivante :
V = π/4 x d² x h
Surface et superficie d’un terrain : ares et hectares
Pour la surface d’un terrain, on parle de superficie plutôt que d’aire, et on utilise l’are (symbole a) et l’hectare (symbole ha) plutôt que le mètre carré (m²) ou le kilomètre carré (km²) :
- Un are est égal à 100 m², soit l’équivalent d’un carré de 10 mètres de côté.
- Un hectare est égal à 100 ares ou encore 10 000 m², soit l’équivalent d’un carré de 100 mètres de côté.
Théorème de Pythagore
Théorème de Pythagore : dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit.
c² = a² + b²
Aire et surface d’un triangle isocèle
Un triangle isocèle est un triangle ayant au moins deux côtés de même longueur. Si b est la longueur de ces deux côtés et a la longueur du troisième côté, alors l’aire A correspondant à la surface de ce triangle isocèle est égale à :
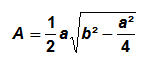
Un triangle isocèle ayant les propriétés d’un triangle quelconque, si h est la hauteur du triangle isocèle, son aire A est égale à :
A = a x h / 2
Aire et surface d’un triangle équilatéral
Un triangle équilatéral est un triangle dont les trois côtés sont égaux. Si a est la longueur de ces trois côtés, l’aire A correspondant à la surface de ce triangle équilatéral est égale à :
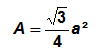
Un triangle équilatéral ayant les propriétés d’un triangle quelconque, si h est la hauteur du triangle équilatéral, son aire A est égale à :
A = a x h / 2
Aire et surface d’un parallélogramme
Un parallélogramme est une figure à quatre côtés. Dans un parallélogramme, les côtés opposés deux à deux ont la même longueur et sont parallèles. Si l est la longueur d’un de ces côtés, et h est la hauteur du parallélogramme, alors l’aire A de la surface correspondant à ce parallélogramme est égale à :
A = h x l