LeMemento.fr

Un angle exprime l’inclinaison d’une droite par rapport à une autre, ou d’un segment par rapport à un autre. Les angles sont habituellement notés avec les lettres grecques α (alpha), β (beta), γ (gamma), …

Les principales unités de mesure sont :

• Le degré
• Le radian
• Le grade
• Le tour

Le degré

Par définition, un degré (symbole °) correspond au 1/360ème d’un angle plein (tour complet).

Les sous-unités du degré sont :

• La minute (symbole ‘) : 1° = 60’
• La seconde (symbole ″) :  1′ = 60″, 1° = 3600″

La notation d’un angle sous forme d’un réel peut être utilisée. Ainsi un angle de 15° 6′ peut également s’écrire 15,1°.

Angles remarquables :

• Angle nul : 0°
• Angle droit : 90°
• Angle plat : 180°
• Angle plein : 360°

La mesure d’un angle en degrés est héritée des babyloniens qui avaient un système de numérotation en base 60. Les arabes ont ensuite utilisé le degré pour mesurer les angles astronomiques. Une année valant environ 360 jours, la rotation de la terre autour du soleil s’effectue avec un angle approximatif d’un degré par jour. La mesure du temps en a découlé, d’où la subdivision de l’heure en minutes et secondes.

Du fait que la valeur 360 est divisible par un grand nombre d’entiers, beaucoup d’angles remarquables peuvent être exprimés sous la forme d’un entier et  le degré est une unité d’angle aujourd’hui très largement utilisée.

Le radian

Le radian (symbole rad) se défini par rapport au nombre π (PI). Un tour complet vaut 2π.

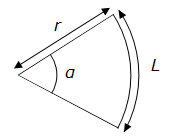
Cette unité est très utilisée en mathématiques car est permet une relation directe entre un angle exprimé en radians et la longueur d’un arc de cercle associé. Ainsi, pour un cercle de rayon 1, la longueur d’un arc de cercle est égale à l’angle exprimé en radians.

De façon plus globale, la relation entre la longueur L d’un arc de cercle de rayon r et l’angle associé α exprimé en radians est égale à :

L = rα

 

Angles remarquables :

• Angle nul : 0 rad
• Angle droit : π/2 rad
• Angle plat : π rad
• Angle plein : 2π rad

Le grade

Le symbole du grade est « gon » (de gônia, qui signifie angle en grec) depuis le décret n°82-203 du 26 Février 1982. L’ancien symbole « gr » est toutefois encore largement utilisé pour les angles exprimés en grades. Par définition, un tour complet de subdivise en 400 grades.

Angles remarquables :

• Angle nul : 0 gon
• Angle droit : 100 gon
• Angle plat : 200 gon
• Angle plein : 400 gon

Le grade a été défini à partir du mètre, qui est lui-même le dix-millionième du quart d’un méridien. La terre ayant un circonférence d’environ 40 000 km, et un angle plein étant équivalent à 400 gon, 1 gon représente une distance de 100km sur la surface de la terre. Le grade est principalement utilisé en topographie, pour la navigation maritime et le tracé des cartes d’état-major.

Cependant, avec le grade, des angles couramment utilisés comme par exemple le tiers d’un tour ne correspondent pas à des valeurs entières. C’est pourquoi cette unité est de moins en moins utilisée.

Le tour

Le tour (symbole tr) est l’unité de mesure d’angle la plus simple à comprendre (exemple : rotation d’un quart de tour dans le sens des aiguilles d’une montre). Elle est surtout utilisée en mécanique, mais parfois aussi en physique et en mathématiques.

Angles remarquables :

• Angle nul : 0 tr
• Angle droit : 1/4 tr
• Angle plat : 1/2 tr
• Angle plein : 1 tr

Table de correspondance des différentes unités d’angle

La table de conversion ci-dessous donne la correspondance entre les principales unités d’angle :

Angles	Tours	Degrés	Radians	Grades
Angle nul	0 tr	0°	0 rad	0 gon
	1/12 tr	30°	π/6 rad	33,333… gon
	1/8 tr	45°	π/4 rad	50 gon
	1/6 tr	60°	π/3 rad	66,666… gon
Angle droit	1/4 tr	90°	π/2 rad	100 gon
	1/3 tr	120°	2π/3 rad	133,333… gon
Angle plat	1/2 tr	180°	π rad	200 gon
Angle plein	1 tr	360°	2π rad	400 gon

Pour la conversion d’unités de mesure d’angle, nous vous invitons à utiliser notre convertisseur d’angles.

Classification des angles

Les angles peuvent être classifiés selon les critères suivants:

• Un angle rentrant est un angle supérieur à l’angle plat (valeur d’angle comprise entre 180° et 360°).
• Un angle saillant est un angle inférieur à l’angle plat (valeur d’angle comprise entre 0 et 180°)
• Un angle saillant est obtus lorsqu’il est supérieur à l’angle droit (valeur d’angle comprise entre 90° et 180°)
• Un angle saillant est aigu lorsqu’il est inférieur à l’angle droit (valeur d’angle inférieure à 90°)

Il existe également des termes relatifs à la relation entre deux angles :

• Deux angles sont dits complémentaires lorsque leur somme est égale à 90°.
• Deux angles sont dits supplémentaires lorsque leur somme est égale à 180 °.