Aire et surface d’un cylindre
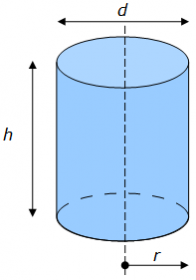
Soit un cylindre de hauteur h et de rayon r.
L’aire A1 correspondant à la surface latérale (ou partie courbe) de ce cylindre est calculée à partir de la formule suivante :
A1 = 2πrh
L’aire A2 correspondant à la surface totale de ce cylindre (surface latérale et extrémités du cylindre) est calculée à partir de la formule suivante :
A2 = 2πr (h + r)
En considérant le diamètre d du cylindre plutôt que son rayon r (sachant que d = 2r), les formules pour le calcul de l’aire d’un cylindre deviennent :
A1 = πdh
A2 = πd (h + d/2)
Remarque :
La hauteur et le rayon (ou diamètre) du cylindre doivent être exprimés dans la même unité de longueur (par exemple en centimètres). L’aire du cylindre sera alors exprimée dans cette même unité au carré (des cm² dans notre exemple).
Principe de calcul de l’aire d’un cylindre
Aire de la partie courbe ou surface latérale d’un cylindre :
La surface latérale du cylindre correspond à un rectangle (enroulé autour du cylindre) dont la hauteur est h et la largeur est égale à la circonférence du cercle de rayon r.
En appliquant la formule pour le calcul de la circonférence d’un cercle (2πr ou πd) et celle pour le calcul de l’aire d’un rectangle (hauteur x largeur) on obtient donc pour le calcul de l’aire A1 de la surface latérale d’un cylindre :
A1 = 2πr x h = πd x h
Surface totale d’un cylindre :
La surface totale d’un cylindre est la somme de la surface latérale et de la surface des deux extrémités de ce cylindre.
L’aire d’une extrémité de ce cylindre correspond à l’aire d’un disque de rayon r ou de diamètre d, soit πr² ou πd²/4. Ce résultat est à multiplier par deux pour prendre en compte les deux extrémités du cylindre.
L’aire A2 représentant la surface totale d’un cylindre de hauteur h et de rayon r se calcule donc à partir de la formule suivante :
A2 = A1 + 2πr²
=> A2 = 2πr x h + 2πr²
=> A2 = 2πr (h + r)
ou en considérant le diamètre d du cylindre (r = d/2):
A2 = A1 + 2πd²/4
=> A2 = πd x h + πd²/2
=> A2 = πd (h + d/2)
Exemple
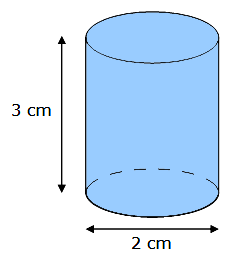
Soit un cylindre dont la hauteur h est égale à 3 cm, et le diamètre d est de 2 cm.
L’aire A1 correspondant à la surface latérale de ce cylindre est égale à :
A1 = πdh = 6π ≈ 18,85 cm²
L’aire A2 correspondant à la surface extérieure totale du cylindre (surface latérale et extrémités) est égale à :
A2 = πd (h + d/2) = 8π ≈ 25,13 cm²
Sur le même sujet :
À lire aussi :